
There is always a lot of talk about QRP vs QRO, 5 watts vs 10, ad nauseam. So today I thought I would run the numbers and see what the real deal is. First we need a few definitions. An S-unit in general terms is the minimum change in signal strength to be just noticeable (k3wwp.com). In more technical terms it equates to approximately 6 db in change. The decibel (dB) is a logarithmic number. Each 10 dB represents a factor of 10 difference. This may be a little out there for some so we will cut right to the shortcut. There are two types of logarithms. For calculating dB, use the common logarithm which is base 10. To see if your calculator uses the right one. Punch in 100 and then log. The answer should be 2 which equates to 10 to the second power which equals 100. This is not a technical paper but an entry way to see how changing the power levels affect the signal level of your transmitting signal. As you guessed, it is not linear.
Let me introduce an equation:
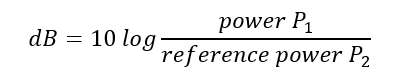
Where Power P1 is the power you wish to evaluate and reference power P2 is your starting power. Let’s take going from 5 watts to 10 watts. The equation would look like this:
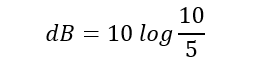
We take 10 and divide it by 5 which give us 2. Then we hit the log function on our calculator which gives us 0.301. Multiply that by 10 and you have about 3 dB in gain or about one half of an S-unit (remember 1 S-unit is equal to 6 dB). Let’s do one more by hand and tackle the QRP/QRO debate. How many S-units will increasing power from 5 watts to 100 watts give you? The equation looks like this:
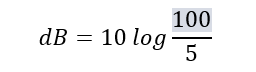
Take the 100 and divide by 5 to give you 20 and then hit the log function to give you 1.301. Multiply by 10 for 13.01 dB. Divide 13.01 by 6 dB and you have 2.17 S-units. Going back to our definition that one S-unit is the minimum change in signal strength to be just noticeable shows that going from 5 watts to 100 watts is not that great of a change.
Let’s let the other shoe drop. What about going from 5 watts to 1500 watt? That will give you 4.13 S-units of gain vs 1.96 S-units going from 100 watts to 1500 watts?
This gives you a fairly easy equation to help you evaluate your needs based upon empirical data. Running 20 watts over 5 gives you 1 S-Unit. Using less power means less drain on the battery for longer operation. This is only part of the equation. Propagation, antenna, mode used, and station efficiency all play a part. Have fun and maybe don’t toss the QRP radio yet 🙂

It’s been a long time since I looked at these formulas. Thanks for the refresher.
LikeLike
I’ve heard this argument presented quite a bit and I agree with it. It is based on the idea that an S-unit is the amount of change in signal which is barely noticeable to the human ear. I think it’s a perfectly valid argument when applied to the human senses. I’ve played similar games with getting 1500W stations to lower their power until I could hear a difference. Typically they have to get down to about 15W or so before there is any noticeable degradation.
It applies with sight as well as hearing. In my wabbitry I have a light tree with two very bright LED lamps. They both put out the same amount of light. I can turn on one lamp and it lights up the whole place. If I turn on the other lamp, one would expect it to be twice as bright. And, technically, if you were to measure the light output with scientific instruments, it probly WOULD measure twice as bright. However, the human senses are weird. When I turn on the second lamp, the change in brightness is barely noticeable: a mere 3db increase, or half and S-unit. I suspect that this is the same phenomenon we see with the S-unit and our hearing. I totally agree with the S-unit argument when applied to voice or CW traffic on the radio, when there is reliance on the human ear.
Now, the question is, what about digital modes? It ISNT our human senses listening to the signal. It’s seems more like the scientific measuring device in the lighting example above. Since the S-unit phenomenon is a function of our human ears, i.e., our perception of the signal strength and not an actual measurement of it, it doesn’t seem like this phenomenon is necessarily applicable to digital modes since it’s the “ears” of the radio and the computer doing the listening and not human hears (which actually cause the S-unit effect).
So does the S-unit argument apply to digital modes? And why. I appreciate your analysis and your thoughts.
LikeLike
My answer would be yes. Only the level of acquisition would change. Voice would be approx. +1 S-unit above the noise. CW would be approx. -1 S-unit below the noise and other digital modes would be approx -2 to -3 S-units below the noise. It’s all relative and the S-unit is common to almost all transceiver meters. It is easy to convert S-unit to dB and back.
LikeLike